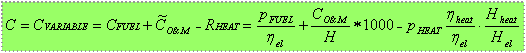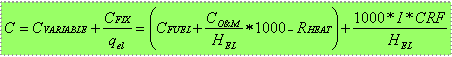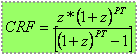Dynamic cost-resource curves - Methodology for model implementation in Green-X

In the model Green-X generation costs and corresponding potentials of all RES-E options (for each country) are described by ‘dynamic cost-resource curves’ being subject to this explanation. Firstly, the calculation of electricity generation costs from RES will be explained, followed by a description of the potentials. Finally, the methodology used for the specification of dynamic ‘cost-resource curves’ is outlined.

Calculation of electricity generation costs

When calculating the generation costs a distinction must be made between already installed and potentially new plants. For existing plants, the running costs (short-run marginal costs) are relevant only for the economic decision whether or not to use the plant for electricity generation. On contrary, for new capacities the long-run marginal costs are important.

Existing plants

The annual running costs are split into two parts: fuel costs and operation/maintenance (O&M) costs. The fuel costs are a function of the fuel price of the primary energy carrier and the efficiency. In the toolbox Green-X, the O&M-costs must refer to the electricity output. Hence, the O&M costs, referring to the energy unit in the database, must be coupled with the full-load hours.[1] In general, one average operation time (full-load hour) is taken for each technology band. Analytically, the generation costs for existing plants are given by:

	(1)
where:

C....................... Generation costs per kWh [€/MWh]

C_VARIABLE ............. Running costs per energy unit [€/MWh]

C_FUEL ................. Fuel costs per energy unit [€/MWh]

 .............. Operation and maintenance costs per energy unit [€/MWh]

C_O&M ................. Operation and maintenance costs per energy unit [€/(kW*a)]

R_HEAT ................. Revenues gained from purchase of heat [€/MWh]

p_FUEL.................. Fuel price primary energy carrier [€/MWh_primary]

p_HEAT.................. Heat price [€/MWh_heat]

h_el...................... Efficiency – electricity generation [1]

h_heat.................... Efficiency – heat generation [1]

H_el..................... Full-load hours – electricity generation [h/a]

H_heat................... Full-load hours – heat generation [h/a]

General remarks:

-	Apart from all kinds of biomass (biogas, solid biomass, sewage and landfill gas), renewables have zero fuel costs, so running costs are determined by operation & maintenance costs only. Therefore the running costs for RES-E are normally low compared to fossil fuels.
-	In the toolbox Green-X, primary fuel prices are given exogenously on a yearly basis. For the sensitivity analysis, however, these default values can be adapted.
-	In the case of simultaneous electricity and heat generation (i.e. CHP), electricity generation costs are calculated by considering the revenues gained from the purchase of the heat.

New plants

The calculation of the generation costs of electricity consists of two parts, variable costs and fixed costs. In more detail, the generation costs are given by:

	(2)
	(3)
where:

C....................... Electricity generation costs per kWh [€/MWh]

q_el...................... Quantity of electricity generation [MWh/a]

C_VARIABLE ............. Running costs per energy unit [€/MWh]

C_FIX ................... Fixed costs [€]

C_FIX / q_el.............. Fixed costs per energy unit [€/MWh]

C_FUEL ................. Fuel costs per energy unit [€/MWh]

C_O&M ................. Operation and maintenance costs per energy unit [€/(kW*a)]

R_HEAT.................. Revenues gained from sales of heat[2] [€/MWh]

I........................ Investment costs per kW [€/kW]

CRF................... Capital recovery factor:             

z....................... Weighted average cost of capital [1]

PT..................... Payback time of the plant [a]

H_EL..................... Full-load hours electricity generation [h/a]

A more detailed description of the running costs is given in the previous chapter. Fixed costs occur independently whether or not the plant generates electricity. These costs are determined by investment costs (I) and the capital recovery factor (CRF).

Investment Costs I

The investment costs differ by technology and energy source. In general, investment costs per unit capacity for RES-E are higher than for conventional technologies based on fossil fuels. Also differences occur between RES-E technologies, e.g. investment costs per unit capacity for small hydropower plants are generally at least twice those for wind turbines. Since most RES-E technologies (with the exception of (large-scale) hydropower) are still not mature, investment costs decrease over time. This evolution is taken into consideration in the toolbox Green-X, i.e. investment costs are derived annually.[3]

Capital recovery factor CRF

The CRF allows investment costs incurred in the construction phase of a plant to be discounted. The amount depends on the interest rate and the payback time of the plant. For the standard calculation of the generation costs these factors are set for all technologies as follows:

-	payback time (PT) of all plants: 15 years
-	weighted average cost of capital (z) = 6.5%.

Note, in the toolbox Green-X, different interest rates will be applied. The interest rate depends on stakeholder behaviour and is a function of guaranteed political planning horizon, promotion scheme, technology, investor category.

General remarks:

-	As the generation costs are calculated per energy output, the fixed costs must also be related to electricity generation qel, compare equation (2). Hence, the fixed costs per unit output are lower if the operation time of the plant ‑ characterised by the full load-hours ‑ is high. payback time (PT) of all plants: 15 years
-	Deriving the generation costs for CHP plants is similar to the calculation for plants producing electricity only. Beside the short-term marginal costs, i.e. the variable costs, fixed costs must be considered for new plants. Of course, equivalent to the case for existing plants, variable costs differ between CHP and conventional electricity plants, as the revenue from purchasing heat power must be considered in the first case.
-	In general, no taxes are included in the various cost-components.

Determination of the (additional) mid-term potential

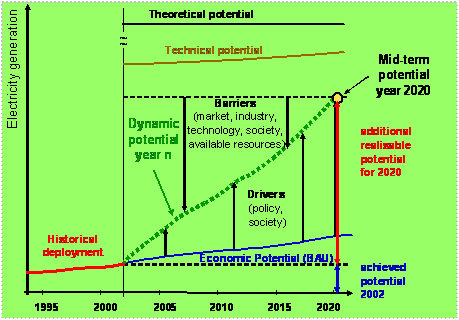
The starting point for deriving the dynamic potential is the determination of the additional mid-term potential for electricity generation for a specific technology in a specific country. The additional mid-term potential is the maximal additional achievable potential assuming that all existing barriers can be overcome and all driving forces are active. The so-called ‘dynamic potential’ is the maximal achievable potential for the year n. This means advantage must have been taken of all existing promotion strategies both on the investor and the consumer side. To illustrate this more clearly, the connections between the different potential terms are depicted in Figure 1 below.

Figure 1. Methodology for the definition of different potentials

In the toolbox Green-X the additional mid-term potential for electricity generation refers to the year 2020. The methodology for the analysis of the potential varies significantly from one technology to another.

-

In most cases a ‘top-down’ approach is used (e.g. for wind energy, photovoltaics). In a first step the technical potential for one technology in one country for 2020 has to be derived by determining the total useable energy flow of a technology. Secondly, based on step one, the mid-term potential for the year 2020 is determined by taking into consideration the technical feasibility, social acceptance, planning aspects, growth rate of industry and market distortions. The additional mid-term potential is given by the mid-term potential minus existing penetration plus decommissioning of existing plants.

-

For a few technologies, a ‘bottom-up’ approach has been more successful (e.g. for geothermal electricity), i.e. by looking at every single site (or band) where energy production seems possible and by considering various barriers, the additional mid-term potential is derived. The accumulated value of the single band yields the additional potential for one technology in one country.

In this context, one specific problem occurs with respect to biomass. The total primary energy potential for biomass is restricted. The actual distribution among the different options ‑ pure electricity generation, CHP generation, heat generation or biofuel ‑ depends on the net economic condition. As for the economic assessment, various support schemes must be considered, the final decision as to which options will actually be implemented is only feasible after including this step. To solve this problem, the values and the different options are linked in the database.

Development of dynamic cost-resource curves

The general modelling approach to describe both supply-side electricity generation technologies and electricity demand reduction options is to derive dynamic cost-resource curves for each generation and reduction option in the investigated region. Dynamic cost curves are characterised by the fact that the costs as well as the potential for electricity generation / demand reduction can change year by year. The magnitude of these changes is given endogenously in the model, i.e. the difference in the values compared to the previous year depends on the outcome of that year and the (policy) framework conditions set for the simulation year. In principle, the approach is carried out in three steps:

-	The development of static cost-resource curves for each generation (as well as each demand reduction) option, on a technology and country-level;
-	The dynamic assessment, including a dynamic assessment of costs as well as of potential restrictions, in order to derive annual cost-resource curves
-	The derivation of the dynamic cost-resource curve.

Static cost-resource curves

A static cost-resource curve describes the relationship between (categories of) technical available potentials (for example wind energy generation, demand reduction from lighting) and the corresponding (full) costs of utilisation of this potential at this point-of-time. This means, that no dynamic effects are included in static cost-resource curves.

On the supply side a distinction between already existing plants and potentially new ones must be made. For existing plants, the economic conditions are given by the short-term marginal costs and the generation potential is given by the installed capacity times the full-load hours. For new plants the long-run marginal costs are relevant. With respect to the potentials, realisable additional mid-term potentials have been assessed for each RES and conventional generation category by country. They represent the maximal additional achievable potential up to the year 2020 assuming that all existing barriers can be overcome in a dynamic context and all driving forces are active.

The static cost curve on the demand side is characterised by the electricity price level at which it is rational to use energy saving technologies compared to a standard technology as well as the long-term potential of electricity saving.

In the Green-X computer model, for both supply and demand, stepped cost-resource curves are applied. For illustration purpose, on the left-hand side of Figure 2 a theoretically ideal continuous static cost-resource curve for the supply side is depicted, taking into account that every location is slightly different from each other and, hence, looking at all locations e.g. for wind energy in a certain geographic area, a continuous curve emerges after these potentials have been classified and sorted in a least cost way. The stepped function, as shown on the right-hand side of Figure 2, represents a more practical approach. Thereby, sites with similar economic characteristics (e.g. in case of wind, sites with same range of full-load hours) are described by one band and, hence, a stepped curve emerges.

Figure 2. Characteristic run of a static cost-resource curve: Continuous (left-hand side) and stepped function (right-hand side)

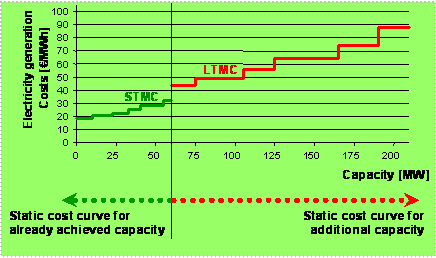
Existing vs. new plant:

As depicted in Figure 3, it is helpful to show a separate development of the cost-resource curve for already existing capacities (i.e. achieved potential) and for potential new plants (i.e. additional potential). In case of existing capacities, short-term marginal generation costs (STMC) (see equation (1)) are relevant for the economic decision whether or not to produce electricity. This is because for existing plants the investments in the capacity are already (irreversibly) sunk. Nevertheless the long-term marginal generation costs are still important for the calculation and evaluation of important results, e.g. the derivation of the producer’s profit. More precisely, as long as the plant is not fully depreciated, the actual investment cost influences (significantly) the actual full generation costs and, hence, the producer’s profit. For new plant, electricity generation costs are determined by the long-term marginal costs (LTMC) (see equation (2) and (3)).

Figure 3. Cost-resource curve for achieved and additional potential of technology x

Dynamic assessment

Dynamics are reflected within the model Green-X on an annual basis. For existing electricity plants and energy saving equipment dynamics is – beside dynamic operation and maintenance costs (fuel prices changes over time according to the selected scenario) – restricted to decommissioning activities of power plants at the end of their lifetime and exchange of energy saving applications, respectively.

For new power plants, dynamic costs and potential information must be derived considering:

-	the selected policy instruments;
-	investor and social behaviour;
-	general framework conditions.

In order to derive dynamic cost-resource curves for each year, a dynamic assessment of the previously described static cost-resource curves is undertaken. It consists of two parts: the dynamic cost assessment and the application of dynamic restrictions (i.e. the dynamic potential assessment).

Dynamic cost assessment

Forecasting technology development is a crucial activity, especially for a long time horizon. Considerable efforts have been made recently to improve the modelling of technology development in energy models. A rather ‘conventional’ approach relies exclusively on exogenous forecasts based on expert judgements of technology development (e.g. efficiency improvements) and economic performance (i.e. described by investment and O&M-costs). Recently, within the scientific community, this has often been replaced by a description of technology-based cost dynamics which allow endogenous forecasts, at least to some extent, of technological change in energy models: This approach of so-called ‘technological learning’ or ‘experience/learning curves’ method takes into account the 'learning by doing / installing / ...' effect.[4]

In general, experience curves describe how costs decline with cumulative production. In this context, the latter is used as an indication for the accumulated experience gained in producing and applying a certain technology. In many cases empirical analysis have proven that costs decline by a constant percentage with each doubling of the units produced or installed, respectively. In Figure 4 the characteristic run of an experience curve is illustrated: As indicated, by plotting such a curve on a log-log scale, a straight line occurs. Thereby, the gradient of the line reflects the corresponding learning rate.

 

Figure 4. Characteristic run of an experience curve: On a linear (left-hand side) and on a log-log scale (right-hand side)
Note: Parameter settings: LR=15%, C0=100.

Forecasting technology development is a crucial activity, especially for a long time horizon. Within the model Green-X the following dynamic cost developments of the electricity generation technologies are considered:

-	Investment costs (experience curves or expert forecast);
-	Operation & Maintenance costs (expert forecast);
-	Improvement of the energy efficiency (expert forecast)

For most technologies the investment cost forecast is based on technological learning (i.e. the appliance of the experience curve approach), see Table 1 below. As learning is taking place on the international level the deployment of a technology on the global level must be considered. Accordingly, learning rates were assumed at least for each decade separately referring to the global development of the considered technology.[5] Within the Green-X model global deployment consists of the following components:

-	Deployment within the EU 15 Member States is endogenously determined, i.e. is derived within the model;
-	For the new EU Member States (EU-10+) forecasts of the future development by RES-E categories are taken from the project 'FORRES 2020' (for details see www.eu.fhg.de/forres);

-	Expected developments in the 'Rest of the world' are based on IEA's 'World Energy Outlook 2004'.

Table 1: Overview of the methodology to derive investment costs for different RES-E options.

RES-E category	Applied approach	Default setting
Biogas	Experience curve (global)	LR (learning rate) = 5%
Biomass (& Biowaste)	Experience curve (global)	LR = 5%
Geothermal electricity	Experience curve (global)	LR = 5%
Hydropower	Expert forecast	No cost decrease in considered period
Photovoltaics	Experience curve (global)	LR = 15% up to 2010, 10% after 2010
Solar thermal electricty	Experience curve (global)	LR = 15% up to 2010, 10% after 2010
Tidal & Wave	Expert forecast	Cost decrease: 5%/year up to 2010, 1%/year afterwards
Wind (on- & offshore)	Experience curve (global)	LR = 9%

Dynamic potential assessment

To derive realisable potentials for each single year of the simulation, dynamic restrictions are applied to the predefined additional realisable mid-term potentials. Thereby, a complex procedure is used, which differs by considered restriction. Default figures which can be adapted within the model, are derived from an in-depth assessment of the historical development of the various RES and conventional generation technologies and the corresponding barriers, which are categorised as follows:

Social barriers:

Social acceptance of additional electricity generation represents an important parameter influencing the penetration of different technologies. In general, a decreasing social acceptance can be observed if penetration of a specific technology increases.^[6] For all generation options social acceptance is considered to be technology specific and will vary form region to region in a country. Figure 5 illustrates the constraint for different barrier levels, which can be edited within the model.

Figure 5. Yearly realisable potential due to social restriction, assuming different barrier levels ‑ low barrier if bS is high, high barrier if bS is low (left-hand side) and resulting maximal deployment of the additional available potential due to social restriction (right-hand side)

Technical barrier:

For the integration of certain decentralised capacity, e.g. wind power, the existing grid represents an important barrier. Grid restrictions lead to longer project lead times and are considered within the Green-X model as technology specific dynamic limitations of the yearly realisable potential on a local (i.e. band) level. As with social barriers, technical obstacles increase with the additional deployment.

Market and administrative constraints:

The maturity of the market represents is one of the key issues influencing the penetration of a technology in the future. In accordance with general diffusion theory, penetration of a market by any new commodity typically follows an 'S-curve' pattern, see Figure 6. The evolution is characterised by a growth, which is nearly exponential at the start and linear at half penetration before it saturates at the maximum penetration level. With regards to the technical estimate of the logistic curve, a novel method has been employed by a simple transformation of the logistic curve from a temporal evolution of the market penetration of a technology to a linear relation between annual penetration and growth rates. This novel procedure for estimating the precise form of the logistic curve is more robust against uncertainties in the historic data. Furthermore, this method allows the determination of the independent parameters of the logistic function by means of simple linear regression instead of nonlinear fits involving the problem of local minima, etc.

In general, market barriers are closely linked to administrative barriers described above and, hence, are described within the model Green-X by one specific indicator on a country-level.

The actual technology-specific growth rates of the market are derived by an econometric analysis conducted for each country and RES-E technology within the EU projects 'FORRES 2020' and Green-X. For each RES-E category the 'best practise' market curve is characterised by those (two) countries with the best performance.

Figure 6. 'S-curve' pattern: Market penetration of a new commodity

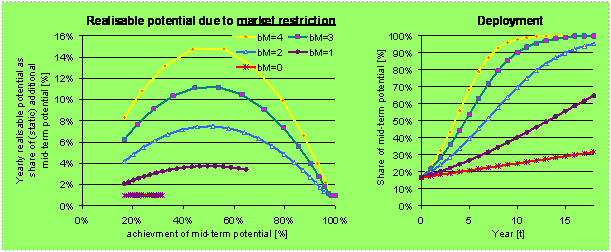
Figure 7. Yearly realisable potential due to market and administration restriction, assuming different barrier levels ‑ low barrier if b_M is high, high barrier if b_M is low (left-hand side) and resulting maximal deployment of the additional available potential due to social restriction (right-hand side)

Figure 7 illustrates the applied approach for different barrier levels: On the left-hand side resulting yearly realisable potential in relation to the applied barrier level and on the right-hand side related deployment – in case that no other constraint would exist – is depicted.

Industrial barriers:

In general, the availability of a certain production technology in one country depends on the total global demand. For example, if the (policy-driven) demand for a certain technology, for example wind power plant, would increase rapidly at the international level, then a bottleneck situation might occur with respect to the industrial production of wind turbines. As a result less capacity could be installed also on a country-level. The limitation of a certain technology is considered in Green-X on an international level.

The actual available yearly potential is obtained by combining the different barriers on the band, country and international level. This means, depending on the already achieved deployment rate, different barriers limit the additional yearly available potential.

The assessment on the demand-side is less complex compared to the supply side, because the existing barriers and obstacles are given exogenously in the model Green-X, i.e. they are not derived within the simulation process. Nevertheless, yearly dynamic restrictions of the total technology specific energy saving potentials can vary over time and depend on the already additionally achieved potential of this certain technology in the sector and country.

Dynamic cost-resource curve

The technology and country-specific dynamic cost-resources for the simulation year are derived by combining the static cost-resource curves with the dynamic assessment. This dynamic cost-resource curve on the supply side contains information about actual generation costs and the possible potential for electricity generation for various technologies for the simulation year. Figure 8 illustrates this procedure for one technology on the supply side.

Similarly, a dynamic cost-resource curve on the demand side contains technology specific information about the electricity price level, at which it is cost efficient to use electricity saving technologies and the possible potential for electricity demand reduction for the simulated year.

Figure 8. Method of approach regarding dynamic cost-resource curves for RES-E